Stability test: Existence, Uniqueness, and Stability Problem

Stability test

A stability test is a type of scientific experiment used to determine a system’s stability. This can be done by putting the system through different tests or putting outside forces or influences on it to see how it responds. A stability test aims to find any possible sources of instability in the system and to understand how the system responds to different disturbances or conditions.


For example, a stability test might be done on a bridge to see how it reacts to different loads or winds in order to determine how stable its structure is. A stability test in a biological system might involve exposing the system to various temperatures or levels of light to see how it responds in order to determine its ecological stability.


As part of a stability test for an economic system, different market conditions or policy changes may be made to see how the system responds. This helps to figure out how stable the system is. Overall, stability tests are an important tool for understanding a system’s stability and identifying potential sources of instability that may need to be addressed to keep the system stable.

Existence, Uniqueness, and Stability Problem

In economics, general equilibrium refers to a state of balance in which all markets in an economy are simultaneously balanced. However, this concept can lead to several issues, including:

  1. Existence: One issue with the concept of general equilibrium is that it is not always true. In some cases, it may be impossible for all markets in an economy to be in equilibrium simultaneously. This is because different markets interact in complex ways, and economic decisions are always made in the face of uncertainty.
  2. Uniqueness: Even if general equilibrium exists, there may be more than one way for an economy to be in equilibrium. This means that it may not be clear which state of equilibrium is the “correct” one, and different economists may have different views on this question.
  3. Stability: Another problem with general equilibrium is that it may not always be stable. In some cases, small changes in one market can have cascading effects on other markets, causing the economy as a whole to move away from equilibrium. This can lead to instability and unpredictability in the economy.

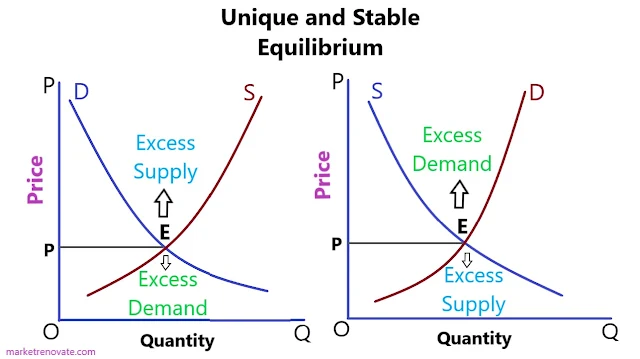
Supply and demand for a particular good or service may sometimes not be perfectly balanced. This can lead to the market having too much of one thing or too little of another. For example, if the demand for a good exceeds the supply, there will be excess demand, and the market price of the good will rise if the supply of a good exceeds the demand, excess supply results, and the market price of the good falls. In either case, the market will be out of balance until either the excess supply or demand is resolved.


Externalities can also be a problem when it comes to general equilibrium. An externality is a cost or benefit that is not reflected in a product’s or service’s market price. For example, if a factory emits pollution as a byproduct of its manufacturing process, this pollution is an externality. If the cost of pollution is not reflected in the market price of the factory’s output, the market will be out of balance.


Another thing that can lead to a general equilibrium like the first is incomplete markets. In a market economy, not all goods and services are traded on markets, and not all resources are distributed via market mechanisms. This can prevent the economy from reaching general equilibrium because the missing markets and resources are not accounted for in the prices and amounts that comprise general equilibrium.


The partial equilibrium model of demand and supply can be used to explain how the three problems of the general equilibrium stability test can be solved. The partial equilibrium demand and supply model is a simplified way to examine the balance in a single market. The economy is assumed to be in general equilibrium in this model, with all markets except the market under consideration in equilibrium.


In economics, when using the partial equilibrium model to look at a general equilibrium, one problem that can come up is the assumption that prices are always the same in every market except the one being looked at. In reality, prices may be changing in other markets because of changes in supply and demand, which may affect the balance in the market. This can cause issues with the existence, uniqueness, and stability of the equilibrium in the market under consideration.


For example, suppose the price of a good that is an input to the production of the good under consideration rises. In that case, the supply of the good under consideration will be affected, potentially disrupting its equilibrium. Depending on the circumstances, this could result in multiple market equilibria or no equilibrium at all. Furthermore, price changes in other markets can make the equilibrium in the market being studied unstable, indicating that it is vulnerable to disruption by external forces or influences.


Another issue that can come up is the idea that quantities are the same in all markets except the one being looked at. In reality, changes in the quantities traded in other markets can impact the equilibrium in the market under consideration.


For example, if the amount of a good that can be used as a substitute for the good being looked at goes up, this will change the demand for the good being looked at and could throw it out of balance. This could make it hard to find a unique and stable balance in the market.


We can examine the problem of existence, uniqueness, and stability with the following example of a demand-supply model.

stability-test-existence-uniqueness-and-stability-figure-1

The above diagram shows that the equilibrium price is (P) where Qd = Qs, meaning neither demand nor supply is too high. The equilibrium price is the price at which the market is cleared. Negative excess demand is defined as excess demand.


An equilibrium price is a price at which no more demand can be met. The equilibrium is stable if the demand function intersects the supply function from above. Excess demand causes price increases in this scenario, while excess supply (also known as excess negative demand) causes price decreases.

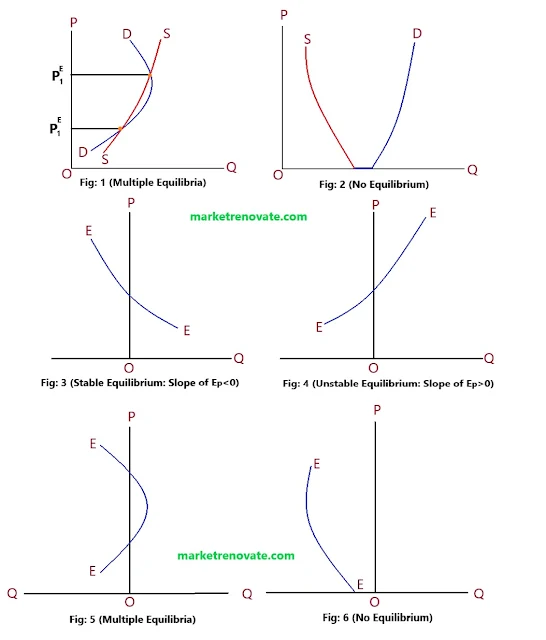
stability-test-existence-uniqueness-and-stability-figure-2

Figure 1 depicts multiple equilibria, with Pe1 stable and Pe2 unstable. Figure 2 lacks an equilibrium at a positive price. We can draw out the following three conclusions from the above diagram:

  1. The existence of equilibrium depends on whether consumers and producers ensure that the demand and supply curves intersect positively.
  2. The slopes of the demand and supply curves determine the stability of equilibrium.
  3. Furthermore, the slope of the excess demand function, which shows the difference between QD and Qs at a given price, determines the uniqueness of the equilibrium.


The excess demand function can answer fundamental questions about equilibrium, such as its existence, stability, and uniqueness. This function is defined as E(Pi) = QD(Pi) — Qs(Pi).


In terms of equilibrium’s existence, stability, and uniqueness, the conclusions we can draw from figures 1–6 can help us understand how markets work. First, we can see that the excess demand function crosses the vertical axis at the equilibrium point, where neither demand nor supply is too high. Second, the number of equilibria equals the number of points where the excess demand curve intersects the vertical axis.


Third, the stability of the equilibrium is based on how steep the excess demand curve is at the point where it meets the vertical axis. If the slope is negative, the equilibrium is stable; otherwise, it is unstable. Finally, there is no equilibrium if the excess demand function does not intersect the vertical axis.


We can use Figures 1 through 6 to draw the following conclusions:

  1. When the excess demand (EP) is zero, the excess demand function (EP) intersects the vertical axis (price-axis). i.e, when QD = Qs, EP = 0.
  2. As shown in Figure 5, the number of equilibria is equal to the number of times the excess demand curve EP intersects the vertical price axis.
  3. The equilibrium is stable when the slope of the excess demand curve is negative at the price-axis intersection point, as shown in Figure 3.
  4. When the slope of the excess demand curve is positive at the intersection point with the price axis, as shown in Figure 4, the equilibrium is unstable.
  5. There is no equilibrium if the excess demand function does not intersect the vertical axis at any price, as shown in Figure 6.

These findings can be applied to general equilibrium analysis, which can help us understand market behavior and the conditions required to reach an equilibrium state.

You Might Like These Posts:
Categories:
GP Sir

GP Sir

GP Chudal is a distinguished educator and scholar with a profound academic background and a passion for teaching. He holds an M.Phil. in Economics, along with Master's degrees in Economics, Rural Development, and Political Science. Additionally, he has a Bachelor of Education (B.Ed.), which underscores his dedication to pedagogical excellence. With this extensive and diverse academic foundation, he brings a wealth of knowledge and interdisciplinary insights to his students.

You may like these posts

Show more

Post a Comment

0 Comments
* Please Don't Spam Here. All the Comments are Reviewed by Admin.

If this article has helped you, please leave a comment.